
En su último programa, Paenza presentó un problema divertido: dos personas se ponen a jugar a la ruleta rusa con un revolver que tiene una capacidad para cargar 6 balas, pero sólo se la cargó con 3 balas. Además, las balas están las tres juntas, una a continuación de la otra. El juego termina cuando queda sólo un participante.

La pregunta es: ¿Quién tiene más probabilidad de sobrevivir: el que toma el primer turno o el segundo? ¿O es indiferente quién empiece?
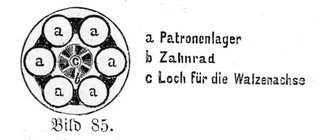
Otra pregunta es: ¿Es posible encontrar una expresión para la probabilidad de sobrevivir si se usa un revolver con capacidad para n balas, cargado con k balas puestas una a continuación de la otra?

3 comments:
Pero el tambor tiene que girar, así es el juego.
Igualmente el primero tiene menos chances de vivir, 1/3, como dijiste, y la fórmula general también está bien (¡creo!) así que posiblemente el razonamiento sea equivalente.
Una forma de pensarlo es ver todas las configuraciones de tambor posibles, que son 6:
1) 111000
2) 011100
3) 001110
4) 000111
5) 100011
6) 110001
donde
0 = click!
1 = bang!
De esas 6 formas posibles, en 1, 3, 5 y 6 pierde el primero:
Prob de perder primero = 4/6
En la 2 y 4 pierde el segundo:
Prob de perder segundo = 2/6
Ah! Ahora sí entiendo! Claro, si giraran antes de cada tiro, siempre es 50 % la posibilidad de zafar.
pero porque? si en el escenario numero 2, el segundo jugador se dispara primero, es decir, gana el primer jugador
Post a Comment