Top Ten

1. Hattori Hanzo y los siete samuráis
2. Tabla y campaña
3. El dilema de Coco
4. El quinteto de la muerte
5. Ladrones de manzanas
6. Galletitas en línea
7. Repostería islandesa
8. Torquemada
9. Teatro independiente
10. La hora en el espejo

Número mágico

Tome un número cualquiera de tres cifras (ABC), invierta el orden de las cifras (CBA), reste el mayor al menor (ABC-CBA o CBA-ABC = DEF), y sume las cifras del resultado (D+E+F). ¿Cuánto da el resultado de la suma? ¿Siempre? ¿Por qué?

Boxeo

Este salió en Página 12, no es muy difícil pero poco intuitivo.

Caren es una boxeadora profesional. Tiene 100 peleas profesionales y un record de 85-10-5 (85 ganadas y 10 perdidas, con cinco empates). Si quiere retirarse con un record con un 90% de peleas ganadas... ¿cuántas peleas más (como mínimo) debe tener?

Probabilidades en la gomería

Resulta que vamos con nuestro auto (un BMW blanco, desde luego) a la Gomería "Las Gomas" y le sacan las cuatro ruedas al vehículo. Luego de una reparación, vuelven a colocar las cuatro ruedas, completamente al azar.

La preguntas es:

¿Cuáles son las probabilidades de que coloquen 4, 3, 2 , 1 o ninguna rueda en su posición original?

Martes 13

¿Es posible que haya un año sin martes 13?

Es más... ¿es posible un año sin "día X", donde "día" es cualquier día de la semana (domingo, lunes, martes, miércoles, jueves, viernes, sábado) y "X" es cualquier número del 1 al 31?

Isabel, Teo & Matías

Ínfima variante del acertijo del suplemento económico Cash de Página/12.

Isabel vive en Olivos y tiene dos novios: Teo, que vive en Belgrano, y Matías, que vive en San Isidro. Para ver a cualquiera de ellos debe tomar el tren de la línea Mitre, Ramal Tigre: para ver a Teo debe tomar el tren que va hacia el sur, y para ver a Matías el que va al norte. Como los quiere a los dos por igual, siempre toma el primer tren que aparece, sin importarle si se dirige al norte o al sur. Sin embargo, el 90 % de la veces termina viendo a Teo.

¿Cómo es esto posible, si los trenes pasan en igual frecuencia para cada dirección?

Tríos de parejas

Supongamos que tenemos estas 6 fichas de dominó:

Preguntas:

1) Si uno toma 2 fichas del total, ¿cuántas parejas distintas pueden formarse?

2) Si uno forma 3 parejas con las seis fichas, ¿cuántos tríos diferentes de parejas pueden conseguirse?

Dominó circular

Siempre es posible formar una trayectoria cerrada con todas las fichas de dominó respetando las reglas de conexión (es decir, conectando los números iguales de dos fichas). La cuestión es: ¿por qué?


Y qué pasa si se sacan todas las fichas que tienen seis puntos. ¿Será posible formar un circuito cerrado? ¿Siempre? ¿Nunca? ¿A veces?

Amebas

Este es un acertijo de Marcia Levitus.

Una determinada especie de amebas se reproduce dividiéndose en dos cada día. Entonces, si hoy tenemos una ameba, mañana tendremos dos, pasado mañana cuatro, etc. Cuando comenzamos con una ameba, se tarda 30 días en llenar una cierta superficie con amebas. ¿Cuánto se tarda en cubrir la misma superficie si comenzamos con dos amebas?

El problema del círculo de Gauss

Vía Juan de Mairena.

Existe una ciudad imaginaria, perfectamente cuadriculada, que se extiende indefinidamente y tiene una plaza cada 6 cuadras. ¿Cuántas plazas hay en un radio de cien cuadras?

CR1P706R4F14

¿Qué dice este mensaje sacado del libro de Paenza?

C13R70 D14 D3 V3R4N0 3574B4 3N L4 PL4Y4 0853RV4ND0 A D05 CH1C45 8R1NC4ND0 3N 14 4R3N4, 357484N 7R484J484ND0 MUCH0 C0N57RUY3ND0 UN C4571LL0 D3 4R3N4 C0N 70RR35, P454D1Z05 0CUL705 Y PU3N735. CU4ND0 357484N 4C484ND0 V1N0 UN4 0L4 D357RUY3ND0 70D0 R3DUC13ND0 3L C4571LL0 4 UN M0N70N D3 4R3N4 Y 35PUM4... P3N53 9U3 D35PU35 DE 74N70 35FU3RZ0 L45 CH1C45 C0M3NZ4R14N 4 L10R4R, P3R0 3N V3Z D3 350, C0RR13R0N P0R L4 P14Y4 R13ND0 Y JU64ND0 Y C0M3NZ4R0N 4 C0N57RU1R 07R0 C4571LL0; C0MPR3ND1 9U3 H4814 4PR3ND1D0 UN4 6R4N L3CC10N; 64574M05 MUCH0 713MP0 D3 NU357R4 V1D4 C0N57RUY3ND0 4L6UN4 C054 P3R0 CU4ND0 M45 74RD3 UN4 0L4 L1364 4 D357RU1R 70D0, S010 P3RM4N3C3 L4 4M1574D, 3L 4M0R Y 3L C4R1Ñ0, Y L45 M4N05 D3 49U3LL05 9U3 50N C4P4C35 D3 H4C3RN05 50NRR31R.

¿Está bueno o no?

Barrilito

Este problema salió publicado en el suplemento económico Cash de Página/12, y es bastante dificil de resolver.

En un almacén hay 6 barriles que contienen 8, 13, 15, 17, 19 y 31 litros de aceite o de vinagre. El litro de aceite cuesta el doble que el de vinagre. Un cliente compra 1400 $ de aceite y 1400 $ de vinagre, dejando sólo un barril.

¿Qué barril quedó?

La decadencia del ingenio

Así se llama el insuperable blog de Jaime. Ahí podrás encontrar, entre muchos posts que seguramente te serán de mucha utilidad, un test para saber de una vez por todas si sos o no sos pelirrojo/a.

Test: ¿Eres pelirrojo?

¿Tienes pecas por todo el cuerpo? ¿Te llamaban Zanahoria (o Zanahorio) en el colegio)? ¿Quizás papafritas con ketchup? ¿La gente sugiere que eres un hijo del diablo? ¿Que traes mala suerte? Conoce la respuesta a estas preguntas contestando a este breve test:

1. Mírate al espejo. ¿De qué color es tu cabello?
a. Rojo.
b. Castaño.
c. Rubio.
d. Otros.

2. Un amigo te pide ayuda para una mudanza.
a. Le ofreces las páginas amarillas para que busque una buena compañía de mudanzas.
b. Te arremangas y comienzas a cargar cajas, estés o no en casa del susodicho (y presunto) amigo.
c. Silbas y te alejas sin darle la espalda.
d. Castaño.

3. Estás acabando un risotto al pesto y no sabes si echarle primero la albahaca o el ajo.
a. Tiras la cacerola a la basura y corres a llorar a tu habitación.
b. Lo consultas en Google.
c. Moreno.
d. Llamas a tu amigo y cedes: le ayudarás en la mudanza. Hay que ver lo que hay que hacer, para eso sirven los amigos, para tocar los cojones.

4. Hace tiempo que no vas a visitar a tus padres. Tu madre te llama llorando y amenaza con desheredarte.
a. Sales del dormitorio, vas a la sala de estar y les saludas.
b. Primero el ajo.
c. Moreno claro.
d. Aceptas ese trabajo en Normandía. ¡Siempre te ha atraído la aventura!

5. Tu color favorito es el:
a. Marrón.
b. Gris.
c. Gris oscuro.
d. Beige.
e. Castaño.
f. Marrón claro.
g. Gris.
h. Otro gris. Ése. Aunque prefiero el rojo. ¿No podías poner colores normales?
i. Rubio.
j. Llamas a tu madre y le prometes que irás a verles el sábado.

6. De niño siempre te disfrazabas de:
a. El sábado sin falta, te lo prometo.
b. Pirata.
c. Vaquero.
d. Bueno, igual el domingo.
e. Nudista.
f. Rubio.
g. Niña
h. Gris.
i. Primero el ajo, hombre.

7. ¿Crees que a veces sólo sabes ver un lado de las cosas?
a. Sí.

8. En el aeropuerto te toman por un terrorista. ¿Cómo reaccionas?
a. Gritas "¡bomba!" entre carcajadas.
b. Castaño.
c. Ya conoces el procedimiento, así que comienzas a quitarte la ropa.
d. Sí.
e. Otros.

9. Vuelve a mirarte al espejo y reconsidera la respuesta a la primera pregunta.
a. Ahora que lo comentas, igual sí que es más rubio oscuro que castaño claro.
b. Beige.
c. Moreno.
d. Rojo.

10. Te invitan a una fiesta, pero te han dicho que él (o ella) estará presente.
a. Prefieres no ir. Le debes demasiado dinero.
b. A y B son correctas.
c. Ninguna de las anteriores.
d. Dos de las posteriores.
e. Sí.
f. Castaño.
g. Las dos y media.
h. Siempre que sea posible.

11. A la hora de comer, prefieres:
a. Carne.
b. Pizza.
c. Creo que el servicio militar no debería ser obligatorio.
d. Di si estás de acuerdo con las siguientes afirmaciones:
d1. Castaño.
d2. Pelirrojo.
d3. Moreno.
d4. Rubio.
d5. Ni ajo ni albahaca, a tomar por culo
e. Pescado.

12. ¿Qué tipo de películas te gustan más?
a. Las de terror.
b. Las románticas.
a. Qué cursi, las románticas dice.
b. Oye, qué pasa, sobre gustos no hay nada escrito.
a. A lo mejor deberías leer más.
c. ¿Me dejáis contestar a mí, o vais a seguir monopolizando las opciones?
a. Perdona.
b. Di.
c. Las comedias.
d. A mí también me gustan las de terror.
c. Tienes que decir otras.
d. Porque tú lo digas.
a. No, es verdad, tienes que decir otras.
d. Bueno, vale, pero por no discutir más, no porque crea que tenéis razón...
c. Va, no te enrolles.
d. Vale, vale, las de acción mismo. Pero para la próxima me pido ser la a.

13. ¿Te consideras una persona demasiado dubitativa?
a. Quizás.
b. Puede.
c. No sé qué decirte.
d. Rubio.

14. ¿Qué opinas acerca de las supersticiones?
a. Que menos mal que has añadido otra pregunta y así no suman 13.
b. Rubio.
c. Yo no soy supersticioso, que eso trae mala suerte... ¡JAAAAA! ¿A que no te sabías esa?
d. Géminis.

Resultados:

Mayoría de a: ¡Felicidades! ¡Eres pelirrojo o pelirroja! O al menos vas teñido o teñida, cosa que no sabremos a ciencia cierta hasta que te veamos en pelota picada, ja, ja.
Mayoría de b: Necesitas esforzarte para llegar a tener el pelo rojo. Te recomendamos que salgas más y que intentes modificar tu ADN. Hoy en día hay muchas clínicas ilegales que prometen milagros.
Entre 45 y 65 puntos: Fíjate en los techos y copia los colores. No tengas en cuenta las tomas de tierra.
Otras: Mides más de metro treinta, cosa que debería llenarte de orgullo y satisfacción.

Química: ¿dónde estás?

En Matemática Episodio 2 de Paenza hay un problemita interesante:

Se tienen dos vasos exactamente iguales con el mismo volumen de líquido. En uno de ellos hay agua pura, en el otro hay alcohol puro. Ahora bien, se toma una cucharada de alcohol del vaso (que tiene el alcohol, obvio) y se la vierte en el vaso que tiene agua. Se revuelve bien, y luego se toma una cucharada (exactamente del mismo volumen que la anterior) de esa mezcla de agua con un poco de alcohol y la vierte en el vaso del alcohol.

La pregunta es: Hay más alcohol en el vaso que tenía agua pura o más agua en el vaso que tenía alcohol puro?

En el problema original se considera vino y agua, lo cual es poco feliz porque el vino tiene mucha agua per se. Paenza propone 3 (tres) formas de resolverlo, pero curiosamente ninguna corresponde al enfoque que utilizaría un químico, que incluyo en los comments.

Parte 3: ¿Quieres ser Pablo Lampone?

3er. TEST

Se cree diferente?? Haga este test.

Alguna vez pensaron si somos iguales o si pensamos las mismas cosas?

Hagan este ejercicio de reflexión y encuentren la respuesta!!!

Siga las instrucciones y responda las preguntas una a una mentalmente y tan rápido como le sea posible. NO SIGA SIN HABER RESPONDIDO LA PREGUNTA ANTERIOR, y se sorprenderá con la respuesta!!!!

Ahora responda una por vez:

Cuánto es:

15+6




3+56




89+2




12+53




75+26




25+52




63+32




Si, estos cálculos mentales no son tan dificiles pero ahora va el verdadero test.




Sea persistente, siga adelante ...




123+5




RÁPIDO!!! PIENSE UNA HERRAMIENTA Y UN COLOR!!




Y vea los comments.

Parte 2: Tengo un chicle en el cerebro

2º TEST

Rápido e impresionante: cuente cuantas letras "F" tiene el texto siguiente.

Sin usar el mouse.

Como siempre, hágalo rápidamente:

FINISHED FILES ARE THE RESULT OF YEARS OF SCIENTIFIC STUDY COMBINED WITH THE EXPERIENCE OF YEARS

Cuántas?

La respuesta en los comments.

Parte 1: Chicles pegados en la cabeza del lado de adentro

Me llegó un mail con una serie de tres "problemas" simples pero interesantes. Es un test para ver si uno es "normal" y, como no lleva más de cinco minutos, vale la pena intentarlo.

Ahí va el primero:

Fue descubierto que nuestro cerebro tiene un "hueco". Aquí va un pequeño ejercicio de cálculo mental. Este cálculo debe ser realizado mentalmente (y rápidamente), sin calculadora, ni papel ni lápiz. Sea honesto, haga los cálculos mentalmente...

Tienes 1000, sumale 40. Sumale 1000 más. Agregale 30 y nuevamente 1000. Sumale 20. Sumale 1000 y añdile 10.

Cuál es el total?

La respuesta está en los comments.

Escrito en la frente

Otro de Paenza, bastante hardcore para mi gusto, así que proponemos acá una versión más facil.

Hay dos personas enfrentadas, cada una tiene un número escrito en la frente. Los números son naturales y consecutivos. Las personas no pueden hacerse señales para comunicarse, sólo están enfrentados pudiendo ver el número el frente del otro, pero obviamente no el suyo.

La pregunta es: Si una de las personas tiene el 2 escrito en la frente ¿puede alguno de los dos deducir que número tiene (respuestas posibles = 1, 2 o 3)?

Una presunta más dificil es: Y si uno de ellos tuviera escrito el número 4 ¿podría alguno de los ellos deducir que número tiene (respuestas posibles = 3, 4 o 5)?

¿Y si tuviera el 666?

Balanza desbalanceada

Tenemos una balanza desequilibrada, como muestra la figura, porque uno de los platillos es más pesado. Tenemos además una pesa de 5 kg y una bolsa con más de 20 kg de azucar. Haciendo sólo dos pesadas: ¿Es posible pesar exactamente 10 kg de azucar? ¿Y 5 kg de azucar?

Ruleta rusa

En su último programa, Paenza presentó un problema divertido: dos personas se ponen a jugar a la ruleta rusa con un revolver que tiene una capacidad para cargar 6 balas, pero sólo se la cargó con 3 balas. Además, las balas están las tres juntas, una a continuación de la otra. El juego termina cuando queda sólo un participante.


La pregunta es: ¿Quién tiene más probabilidad de sobrevivir: el que toma el primer turno o el segundo? ¿O es indiferente quién empiece?


Otra pregunta es: ¿Es posible encontrar una expresión para la probabilidad de sobrevivir si se usa un revolver con capacidad para n balas, cargado con k balas puestas una a continuación de la otra?

Blackjack: cuánto apostar

Usando el sistema hi-lo, un conteo positivo alto indica que es favorable apostar; la cuestión es cuánto. En Rainman, se proponía 1 para conteo desfavorable y 2 para conteo favorable. Una forma un poco más elaborada consiste en considerar que la probabilidad de ganar depende tanto del conteo como de las cartas que aún quedan en el mazo (cuando quedan pocas cartas en el mazo, un conteo positivo es altamente favorable). Entonces, si el conteo es desvaorable, conviene apostar lo mínimo permitido; en cambio, cuando el conteo es favorable, la suma a apostar podría calcularse como:

Apuesta = Valor de la unidad x Conteo / Juegos de cartas en el mazo

El valor de la unidad podría determinarse como la centésima parte del total de dinero disponible al iniciar el juego. Esto es importante por siempre hay que tener resto para seguir apostando.


Para ilustrar este punto consideremos este problema:

Supongamos que un casino pagara 100 a 1 por cada pleno acertado. Esta situación sería muy favorable para los apostadores y, a la larga, el casino siempre perdería dinero. Pero si sólo tuvieramos diez fichas, existe la posibilidad que no acertemos un pleno en diez vueltas de ruleta y, aunque la situación fuera estadísticamente favorable, habremos salido perdiendo.

La pregunta es: ¿Cuál es la probabilidad de no acertar un pleno después de 1, 10, 37 y 100 vueltas de ruleta, apostando una ficha por vuelta?

Tabla y campaña

Rey Carmesí propone un problema interesante:

Dada una tabla de puntuaciones totales por equipo ¿es posible encontrar un método o algoritmo para dar con la combinación de resultados posibles que producirían dichas puntuaciones?

La respuesta es que, en general, no es posible dar con una única combinación de resultados posibles. Consideremos por ejemplo un campeonato como el argentino, con veinte equipos que juegan todos contra todos y supongamos que San Lorenzo le gana a Racing, Racing le gana Vélez y Vélez le gana a San Lorenzo. Esto tendría el mismo efecto sobre la tabla general que si San Lorenzo le ganara a Vélez, Velez le ganara a Racing, y Racing le ganara a San Lorenzo. Por lo tanto, no es posible deducir todos los resultados a partir de la tabla de puntuaciones de los equipos.



Una pregunta más simple es: ¿sería posible a partir de la tabla de puntuaciones totales decir cuántos partidos en total ganó, empató y perdió cada equipo (aunque no los resultados particulares de cada encuentro)?

En otras palabras, es fácil deducir la tabla a partir de la campaña de cada equipo (partidos ganados, empatados y perdidos): ¿es posible el camino inverso?

Blackjack: el sistema hi-lo

Uno de los sistemas más básicos, pero de probada eficacia, para ganar al blackjack es el hi-lo o alto-bajo. Consiste en asignar valores de +1 a todas las cartas del 2 al 6 y -1 para 10JQKA, mientras que las cartas del 7 al 9 son neutras y tienen un valor de cero. Luego hay que ir haciendo la suma de todos los valores de las cartas que van saliendo a la mesa. Un número positivo indica que quedan muchas cartas altas en el mazo y, según la Regla de Oro de Thorp, esta situación favorece al jugador.



La pregunta es: ¿Es posible encontrar una expresión matemática de la probabilidad de ganar en función de la suma de los valores de las cartas? (Es probable que esta pregunta quede sin respuesta a menos que se recurra a simulaciones computacionales complejas.)

La verdad corregida

Si la única verdad es la realidad, entonces la verdad necesita ser corregida. Aquí van nuevos apuntes:

No hay que pedirle peras al olmo, pero a veces es dificil distinguir un olmo de un peral.



De jardines ajenos:

"El tiempo todo locura." Luc

"Mejor bueno por conocer que malo conocido." Kamenetzky

"No sólo sé que nada sé, también sé que sólo sé que nada sé." Hoemro

Albert Einstein usaba una frase de Arthur Schopenhauer para legitimar sus acciones:

"Uno puede hacer lo que quiere, pero no puede querer lo que quiere."

En tanto que Melibé prefiere una de Oscar Wilde:

"La única manera de evitar una tentación es caer en ella."

[Post secuela de éste otro.]

Blackjack: la regla de oro

El blackjack es el único juego en el que es posible a la larga vencer al casino, y esto es así porque lo que ves en la mesa influye sobre lo que vas a ver (por ejemplo, si en la mesa hay un as, entonces hay un as menos en el mazo, y la probabilidad de ver otro as es por ende menor).



En 1963, el profesor del MIT Edward Thorp hizo una simulación del efecto relativo de cada carta sobre las chances de ganar. Lo que encontró es que cuando quedan muchas cartas de valores bajos (de 2 a 7) en el mazo, las probabilidades favorecen a la banca. Por el contrario, si quedan en el mazo más cartas altas (9,10, J, Q, K, A) que bajas, el favorecido es el jugador. En base a este trabajo se desarrollaron muchos sistemas para contar cartas, pero la Regla de Oro para el jugador de blackjack es: cartas bajas en la mesa es bueno, cartas altas en la mesa es malo.

La pregunta es: ¿Será posible encontrar una expresión matemática (una expresión de tipo probabilístico o estadístico) para la Regla de Oro?

Estoy seguro de que este problema es muy dificil, pero sería bueno demostrarla al menos para algún caso particular. Por ejemplo, un juego de 52 cartas (23456789JQKA) para el caso de que hayan 10 cartas en la mesa y 42 en el mazo. Aún así, todavía es muy dificil.

La mirada atenta

...

El binomio de Newton es tan hermoso como la Venus de Milo .
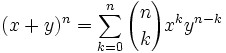Lo que hay es poca gente que lo vea así.

...

(La versión original de estos versos de Fernando Pessoa es: "O binômio de Newton é tão belo como a Vênus de Milo. /O que há é pouca gente para dar por isso.")

1/2 verdades reveladas

“Todas las verdades pasan por tres estadios.

Primero se las ridiculiza.

Luego se lucha violentamente contra ellas.

Por último se las acepta como obvias.”

Arthur Schopenhauer

Los refranes, frases hechas, lugares comunes, aforismos, proverbios, etcétera, etcétera, suelen contener medias verdades, y pocas cosas engañan más que las verdades a medias. Por eso, los que saben recomiendan que, al escuchar esos condesados de sabiduría, se los dé vuelta como un guante, que se los retuerza hasta que tomen una forma nueva, que puede resultar más verdadera, graciosa y elegante.

Algunos ejemplos de reformulaciones de refranes y proverbios:

"Persevera y perseverarás." Marcos

"Mejor rico y sano que pobre y enfermo." Kamenetzky

"Lo bueno si breve, dos veces breve." Bukowski

Con respecto a los aforismos, parece más saludable citar a Oscar Wilde o Ernesto Esteban Etchenique (alter ego de Roberto Fontanarrosa) que a Lichtenberg o Narosky.

Ejemplos de aforismos de Ernesto Esteban Etchenique:

Para el Sabio no existe la riqueza. Para el Virtuoso no existe el poder. Y para el Poderoso no existen ni el Sabio ni el Virtuoso.

Por muy alta que sea una montaña, no sobrepasa su propia cúspide.

Quise conocerme a mi mismo. Cuando me hallé, estaba muy cambiado.

Cuando alcancé la Sabiduría, ella me miró y dijo: “ya me alcanza cualquiera”.

Te señalé el futuro y miraste mi dedo.

Se reciben con gusto otras variantes de refranes populares y nuevos aforismos.

El mundial en el aula

No es novedad que a Felipe no le da placer ir a la escuela:

Por eso no sorpende que Felipe, gobernador de la Provincia de Buenos Aires, haya declarado que "hay que permitir que en las escuelas también haya un momento de placer" (sic sic sic) y, por lo tanto, los alumnos de los colegios bonaerenses podrán ver los partidos de fútbol de la selección argie en el próximo Mundial, en horario de clases. Y argumentó que se debe trabajar este evento en las escuelas para reflexionar sobre temas relacionados, tales como la historia de la humanidad, la geografía y la cosmogonía. Pero el mundial también sirve para plantear problemas de ingenio, como los muy buenos que proponen Markelo y 26. Un muy bien diego para ellos.

Uptade: Aquí los problemas del mundial recopilados por Markelo.

Todos contra todos

Si n equipos jugaran todos contra todos:

¿Cuántos partidos se jugarían?

¿Cuántos puntos podrían sumarse en total entre los obtenidos por todos los equipos?

¿Cuántas tablas de posiciones diferentes podrían obtenerse considerando sólo las posiciones relativas de los equipos?

¿Cuántas combinaciones de resultados (considerando todos los partidos) podrían darse?

Ejemplo para n = 3:

3 partidos; entre 6 y 9 puntos; 6 tablas sin considerar la posibilidad de empates en las posiciones; 27 combinaciones diferentes.

La torre de Pisa

Juan de Mairena está indignadísimo con los daños colaterales que provoca esta guerra mundial sublimada llamada Mundial de Fútbol. Y de un curioso modo googliano, su indignación se deriva hacia absurdos que pueden encontrarse en sitios supuestamente respetables de la web acerca de la torre de Pisa: que su inclinación es del 10%, que se mueve a razón de 9 mm al año, etc. (Nota al margen: para aquellos que se sienten sofocados por el mundial, Guillermo Piro propone algunas alternativas que, debo aclarar, deben tomarse como una sátira humorística -y lo aclararo explicitamente pues este sitio ha sido recomendado como adecuado para niños y adolescentes, y ahora me siento en la responsabilidad de no contribuir a su deformación pues, como ya habrán empezado a notar, éste es un mondo dificile.)

Bueno, volviendo a la torre de Pisa, su inclinación debería indicarse con el ángulo en grados. Pero Juan de Mairena nos indica:

"Según Wikipedia, la altura es de 55.86 m en el lado más alto y 56.70 en el más bajo. ¿Alcanza para calcular la inclinación? Mmm... necesitaríamos el diámetro, pero sólo tenemos el de la base (en dos versiones: externo e interno), pero en la foto vemos que arriba la torre se angosta, así que necesitaríamos el diámetro de la cúpula."

La pregunta es: ¿Es posible encontrar la relación entre el ángulo de inclinación de la torre y el diámetro de la torre con los datos dados?

Otros fixtures

Para resolver mentalmente:

Como está diagramado el fixture del campeonato, en el mundial de fútbol se juegan 64 partidos. Pero...

¿Cuántos se jugarían si jugaran todos contra todos?

¿Y si todos los partidos fueran por eliminación directa (el ganador sigue, el perdedor se va a casa) como es en los torneos de tenis?

De los tres sistemas considerados (todos contra todos, eliminación directa, y el sistema mixto que en definitiva se usa) ¿cuál será el más justo y cuál el más entretenido?

Recordemos que participan 32 equipos.

¡Orsai, referí!

El tema del fuera de juego es uno de los asuntos más delicados del fútbol. Los jueces de línea deben decidir en fracciones de segundo si cuando la pelota parte hacia cierto jugador, éste tiene aún frente a sí o en su misma línea a otros dos jugadores del equipo rival. Por lo general, uno de los jugadores rivales que habilitan la jugada es el arquero, y la cuestión es la posición relativa del atacante respecto del defensor de campo. Esta regla le exige que al juez de línea que controle simultaneamente la posición de la pareja defensor-atacante y la jugada desde donde parte el balón. Para cumplir tal tarea con efectividad, los jueces de línea deberían estar dotados con una dispoción ocular algo bizarra.

El juez de línea debe tener un ojo puesto en la línea de ataque y otro en la pelota.

Éstá claro que determinar un fuera de juego "finito" es dificil sin complicaciones extra. Pero a veces la situación se complica aún más por muchos factores, tales como el corte del césped que se ve en algunos campos de juego, en forma de círculos concéntricos. El corte en franjas rectangulares facilitaría la determinación del fuera de juego, pero los círculos concentricos la dificultan.

Aunque no lo parezca, en esta figura los círculos con concéntricos.

El tema del fuera de juego tampoco se resuelve con el telebeam, puesto que los que lo manejan usan criterios diferentes a los de los jueces de línea. Según el telebeam, por ejemplo, el botín del defensor podría habilitar una jugada, pero los jueces consideran más bien la líena troncal del jugador. Es decir, hay diferencias de criterio respecto a lo que se considera la línea del jugador.

Croto

El matemático Croto se baña todos los sabados (lo crea necesario o no) cuya fecha corresponda a un número primo (el 2 de enero, el 17 de octubre, el 31 de diciembre, etc, si es que caen sabado). ¿Cuántas veces por año, en promedio, se baña Croto?

Planeta fútbol

Este es un problema para resolver mentalmente:

¿Cuántas horas frente al televisor pasaríamos si viesemos todos los partidos del mundial? Supongamos que cada partido lleva en promedio 2 horas, considerando que escuchamos algún himno -a mí me gusta La marsellesa-, el entretiempo, eventuales alargues y definiciones por penales.

Listos para una sobredosis de Tevé

(Por si algún extraterrestre no lo sabe, hay 32 equipos, inicialmente divididos en 8 grupos de 4 equipos que juegan entre sí, luego clasifican 16 equipos a las llaves de eliminación de elimunación directa. Yo hice la cuenta mentalmente y me olvidé de contar el anteúltimo partido.)

La pelea de los gatos

Variante del Problema para la Almohada #4

Un gato en el tejado de la casa mantiene intrigado a Tom Sawyer. No está seguro si es el gato del vecino de la izquierda, que es blanco, o el de la derecha, que es negro. Tom sale al jardín e intenta ver de qué gato se trata, pero está demasiado oscuro. Si pudiera hacer que, de alguna manera, el gato se mueva hacia donde haya más luz, podría saber a de qué gato se trata. Para resolver el problema, Tom busca el gato de la tía Polly, que es blanco. Lo toma de la piernas traseras y describiendo círculos como un lanzador de discos griegos lo arroja sobre el tejado, con muy buena puntería hay que admitir, muy cerca de donde está el otro gato. Se produce entonces una lucha brutal entre ambos gatos.
Realmente es imposible distinguir nada, pero los gritos, gruñidos y choques indican que la pelea es pareja y entretenida, por lo menos hasta que uno de los gatos sale despedido en dirección contraria a donde estaba Tom, que sólo pudo distinguir el color del gato volador. Entonces Tom dice: "No pude distinguir si era el gato de la tía Polly, pero estoy seguro de que era un gato blanco... entonces hay un 66.6 % de probabilidades de que sea el gato del vecino de la izquierda el que estaba, o sigue estando, sobre el tejado." Suponiendo que los dos gatos son luchadores igualmente bravos ¿razonó bien Tom?

Sheik Yerbouti

Variante del problema de Gamow y Stern


Sheik Yerbouti está interesado en aumentar la cantidad de mujeres disponibles para los harenes, por lo cual impusó una ley que prohibe a las mujeres volver a concebir luego de haber dado a luz un hijo varón. Si en cambio concibieron una niña, pueden reincicir en la maternidad con total impunidad. El jeque explicó que de ese modo todas las familias tendrían a lo sumo un hijo varón, pero podrían tener cualquier número de hijas mujeres... con lo cual se conseguía el objetivo fijado.

La pregunta es ¿está en lo correcto Sheik Yerbouti?

Es interesante considerar dos casos diferentes:

a) todas las madres tienen una probabilidad de 1/2 de concebir un hijo varón;

b) el 50% de las madres tiene una probabilidad de 1/3 de concibir varones y el otro 50% tiene 2/3 (de modo que todas las madres en conjunto conservan la probabilidad 1/2 de concebir varones). Esto quiere decir que estamos considerando que existe cierta predisposición (posiblemente genética) para engendrar vástagos de un determinado género.

El quinteto de la muerte

Variante de El hombre que calculaba.

A media noche, el quinteto de la muerte completó con éxito el golpe a la bóveda del casino, llevándose un botín millonario. El dinero está empaquetado en fajos de billetes de a mil dólares, dinero que han ocultado en el sótano y repartirán equitativamente a primera hora de la mañana.

Sin embargo, a las 2 PM, el líder de la banda, y clasisista altamente educado, se levanta y, con el fin de aligerar la tarea de la mañana siguiente, separa el dinero en cinco pilas iguales. Y mientras mira una de las pilas, que le corresponde por derecho, decide que no es una mala idea separar ésa, su pila, del resto, y la oculta. Más tranquilo, después de saber que su dinero está seguro, se va a dormir.

A las 3 PM, el general tiene la misma idea. Ignorante de que su líder ya había hecho la separación de bienes, procede a distribuir el dinero en cinco pilas iguales, toma una de ellas, la oculta y se va a dormir.
A las 4 PM, el infiltrado tiene la misma idea y, sin saber que el líder y el general ya habían hecho la repartija, separa todo el dinero en cinco pilas, toma una, la esconde y se va a dormir.
A las 5 PM, el hombre de los explosivos decide que la cosa más fácil del mundo –y la más inteligente- sería asegurarse su quinto del botin. Y por supuesto, repite el procedimiento de los tres compañeros que le precedieron.

El hombre de la fuerza bruta, en cambio, durmió toda la noche. Tuvo sueños placenteros, en los que anotó varios touchdowns y las porristas lo adoraban y era el chico más popular de la preparatoria.
A la mañana, el hombre de la fuerza bruta se despierta y dice: “llegó la hora de que nos repartamos equitativamente el dinero”. Y los demás, haciéndose los tontos, acuerdan con una sonrisa. Los muchachos se reparten el dinero –materia altamente discutible si es mal habido, pues ladrón que roba ladrón tiene cien años de perdón. Y la pregunta es: ¿cuánto dinero recibió cada uno de los integrantes del quinteto de la muerte y a cuánto ascendió el total del botín?

Repostería islandesa

Variante del Hombre que calculaba.

Lola y Hófí están mirando el canal "El Gourmet" en la casa de Hófí. En la televisón, Jean Pier Noé está dando las indicaciones para preparar una verdadera delicatessen. El plato en cuestión es una tortilla islandesa que requiere del empleo de ocho de huevos de fasián.


Hófí dice: "¡Qué lástima! Sólo tengo 5 huevos de faisán en la nevera." Lola no puede creer lo que son las causualidades, y exclama: "¡No puedo creer lo que son las casualidades, porque yo tengo exactamente 3 huevos de fasián en mi nevera!" Deciden entonces preparar juntas la exquicitez.

Al ir Lola hacia su departamento en busca de los huevos de faisán, se cruza con Hlynur, amigo tanto de Lola como de Hófí. Lola, sabiendo que el solitario Hlynur disfrutaría de una cena tan elaborada, lo invita a comer. Hlynur acepta con la condición de que se le permita hacer algún aporte y, luego de hurgar y revolver en sus bolsillos, saca 80 coronas islandesas.

De regreso en la casa de Hófí, con los 3 huevos de faisán y el invitado Hlynur, Lola le cuenta a Hófí que Hlynur se quedará a la cena pero quiere contribuir con 80 coronas. Y Lola agrega: "Podríamos dividirnos esas 80 coronas entre vos y yo, de modo proporcional a la cantidad de huevos de faisán que aportamos a la tortilla... serían 50 coronas para vos y 30 para mí ¿no es así?". Pero Hófí le contesta: "En todo caso, a mí me corresponderían 70 coronas, y 10 a vos. Pero sugiero que usemos ese dinero para comprar un vino -Jean Pier aconsejó un buen Cabaret Noir, que haría un perfecto maridaje- y alquilemos una película para ver juntos. Mi recomendación es 101 Réikiavik."

A Lola la sugerencia le pareció perfecta, y compartiron luego una velada excelente. Pero a nosotros sólo nos importa saber una cosa: Si Lola, Hófí y Hlynur comieron cada uno 1/3 de la tortilla: ¿cuál hubiera sido la forma correcta de dividirse las 80 coronas entre Lola y Hófí: 30-50 como dijo Lola, o 10-70 como pretendía Hófí?

Teatro independiente

El éxito de la obra de teatro independiente "Amor/Odio" se debe exclusivamente a la difusión "boca a boca". Lo curioso del caso es que en todas las funciones, el 50 % de los espectadores la encontró insoportable, pero al otro 50 % le gustó tanto que no sólo volvió a verla por segunda vez, sino que además consiquió que otra persona lo acompañe a verla. La obra se representa una vez por semana y lleva cinco en cartel. En la primera función hubo dieciseis espectadores...¿cuántas en la última?

Geometría primitiva

Variante del Problema para la Almohada #33

Si el círculo externo tiene un radio de 1, ¿cuál es el radio del cícrculo interno? ¿Puede generalizarse la solución para cualquier figura con n lados?

Torquemada

Este es una variente de otro que contó Chacramont.



Torquemada, líder de la Inquisición, se la tenía jurada a tres hombres sabios, llamados Lavoisier, Bruno y Dalton. Este último padecía de daltonismo, es decir no podía diferenciar los colores.

Torquemada citó a los tres y les planteó su acusación:

"Os creeis grandes hombres, grandes sabios, pero lleváis en la sangre el peor de los pecados, el mismo que hizo caer al ángel a su reino de tinieblas: la soberbia. Pero hoy amanecí piadoso, y os daré una oportunidad. Os plantearé un problema, y si podéis resolverlo, os dejaré libres. Tengo por allí tres gorros rojos y dos gorros verdes, y cada uno de vosotros os pondreis uno de ellos al azar. Cada uno podrá ver únicamente el gorro de los otros dos y tendrá que decir de qué color es el gorro."

Después de que le pusieran los gorros, Torquemada dijo: "Empezá vos, Lavoisier."

Lavoisier observó a sus compañeros y dijo: "Prefiero no decir nada a decir cualquier cosa."

Toquemada respondió: "Su respuesta demuestra un desdén por este tribunal que es inaceptable." Y agregó dirigiendose a sus guardias: "Cortadle la cabeza."

Luego, dijo sin ganas: "Su turno, Bruno."


Bruno observó a los sobreros de Lavoisier y Dalton, y dijo: "Eh... eh... ehhhhhhhh..."

Y Torquemada: "A la hogueeeeeeeeera. Demasiado tarde para dudas, Bruno."

Dalton observó como se llevaban a Bruno, que tenía un gorro que le pareció gris, y la cabeza solitaria de Lavoisier, con un otro gorro que también le pareció gris, cerró los ojos un segundo y dijo ante la mirada entre inquisidora y divertida de un Torquemada que no desconocía el daltonismo de Dalton: "Mi gorro es...". Y dijo el color correcto.

Una vez repuesto de su sorpresa, Torquemada le dijo a sus guardias: "Llevenlón al potro y elonguenlón hasta que confiese que acertó de pura casualidad."

Pero Dalton dijo: "Eso no será necesario." Y en pocas palabras, le explicó como había llegado a una conclusión que no dejaba lugar a dudas acerca del color de su gorro.

Torquemada estaba sorprendido, jugueteó un momento con los dedos y finalmente dijo: "Semejante respuesta no puede considerarse de otro modo que una confesión de su parte del delito que se le imputa (esto es, la soberbia). Es más, tengo la certeza que solamente la serpierte que tentó a Eva puedo haberle inspirado tan diabólico razonamiento. Preparen otra hoguera para el Sr. Dalton."

Torquemada se salió con la suya, pero... ¿de qué color era el sobrero de Dalton y cuál fue el argumento que esgrimió?

El dilema de Coco

Coco es un entrenador de fútbol que dispone de tres delanteros, todos grandes goleadores con un promedio de un gol por partido. Sin embargo, los tres tienen caractrísticas distintas.



Loco es lento y torpe, pero letal. Por lo general, toca la pelota dos veces por partido, pero cuando la toca, la mitad de las veces la pelota termina en el fondo del arco.


Chelo es movedizo y veloz. Se muestra, pide la pelota, participa, dispone de una opción de gol cada nuve minutos de juego, pero su obsesión por definir pegando con "tres dedos" lo convierte en poco efectivo: sólo 1 de 10 son gol.



Melli es un caso intermedio. Es el más inteligente de los tres, pero no tiene la velocidad de Chelo ni la potencia de Loco. Dispone de una chance de gol cada 15 minutos y convierte una de cada seis.

Este es el dilema del Coco: Sólo puede emplear uno de los tres... ¿con qué delantero le conviene jugar si le alcanza con convertir un gol por partido? ¿Y si tuviera que convertir al menos dos goles?

Hatori Hanzo y los siete samuráis

Hatori Hanzo y los siete samuráis se disponen a cenar. Sobre una tabla hay ocho kanikamas, un poco de sake y una horma de queso Casanto. Hatori Hanzo desenvaina su espada samurai y, con tres veloces y precisos movimientos de su katana, corta la horma de queso en ocho porciones exactamente iguales. ¿Cómo lo hizo?